It is important for a new Ph.D. student to understand how reproducibility works and how to contribute to the scientific community with results that are straight-forward to reproduce, and on which future work can be easily based.
Reproducibility has been a big topic in social and medical sciences for a while [1]. There have been few reproducibility crises in the technical world too [2,3]. In this light, it is important for a new Ph.D. student to understand how reproducibility works and how to contribute to the scientific community with results that are straight-forward to reproduce, and on which future work can be easily based. One of the first means on this path is to reproduce a result of important nature on one’s field. That is why I was happy to commence as my supervisor asked me to reproduce the theoretical results of Clayton R. Paul’s “Prediction of Crosstalk Involving Twisted Pairs of Wires-Part I: A Transmission-Line Model for Twisted-Wire Pairs” and compare them with results of a commercial EM-field solver [4].
I started the work on one Friday morning and was able to finish the first version of the paper’s algorithm implemented with MATLAB the same night. Quick results looked fine and I went to spend a weekend with a happy grind on my face. The work was comparable to my B.Sc. thesis work and I was able to get similar progress in a day, compared to a week or two in the earlier phase of my studies. Come Monday and I took closer look at the results. Yes, they looked good at first sight, but were off almost a decade. Logarithmic scale fools one easily. Back to work to go through the code with a tighter comb. Few small mistakes found, but no remarkable change in the results. After spending time with some other activities, like the PETER Kick-Off event [5], it was time to get back to the beef. As the tighter comb for the code did not give any remarkable results, I leaned on deriving some of the equations used in the paper from the beginning with the help of some reference papers [6,7,8]. I got to know some interesting things; like that, the transmission line per-unit-length inductance matrix entries used in the paper are actually derived from the per-unit-length capacitance calculations. For homogenous dielectrics, this is fine as shown in [7], but makes an interesting circular reference as the capacitance matrix is then again calculated from the inductance matrix.
However, no resolution to the inaccuracy problem at hand. The last, nastiest, and most time-consuming resort was to start to go through the matrices and partial results of them. That resulted a nice piece of MATLAB art in Figure 1 to verify that there were no mistakes on the geometry definition. Finally, after a while of banging head to the wall by calculating all kinds of partial results for the matrix equations in question – a simplistic mistake of commutation laws.
Figure 1: Cross-section of one of the test cases
Some of the matrices used were non-invertible, which in this case meant also that they are not commutative and thus sensitive for multiplying either left or right [9]. After this, seemingly small modification, the coefficients for the linear equations were correct and the results started to match nicely with the ones on the paper.
Having used the 3D-simulator CST before, the 3D-modeling part was fairly straight-forward. The results matched well with the analytical formula on the frequency range that the formula was supposed to be effective – and even above. The model example in Figure 2 shows a very good fit. For some other test cases, there were more discrepancies in the results. Most of them were recognized to be caused by different modeling techniques: zero-length twists on the analytical model vs. helix in CST, and calculated per-unit-length inductance and capacitance differences between the two.
As a learning process, I think the exercise was well worth it. As I had a while since my previous academic endeavours, it brought me up to speed nicely. Especially my appreciation grew for a clear writing style with concise markings in equations and the use of quality references for any background checks that the reader might need to do. It is easy to be lazy, but it just decreases the value of one’s work. See reference [9] used in this text as an example. It is only valuable for a very narrow group of readers. Also, a proper grouping and simplification of equations with well thought help variables made finding any of my own errors faster and thus the authors had conveyed the message with the best possible way.
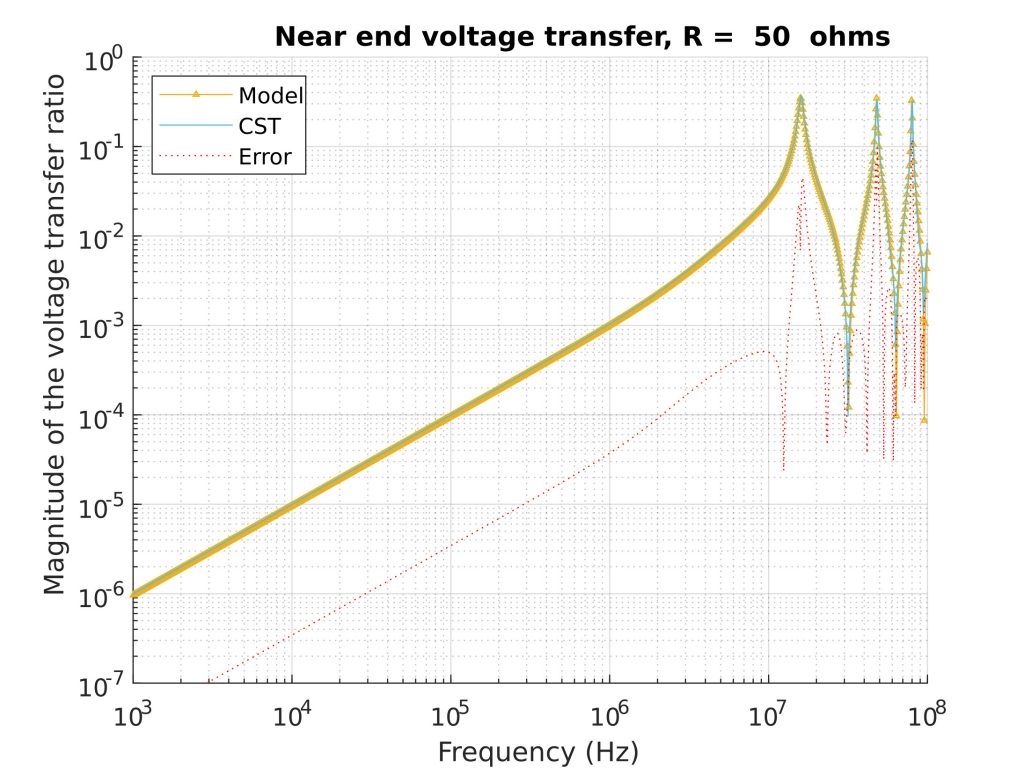
Figure 2: A model example of the results
References
[1] Reproducibility of Scientific Results, Fiona Fidler, John Wilcox. Stan-ford Encyclopedia of Philosophy. Cited on 19.02.2020. https://plato.stanford.edu/entries/scientific-reproducibility/[2] Scandal Rocks Scientific Community, Deutsche Welle. 30.09.2002. https://p.dw.com/p/2i8X
[3] Physicist is found guilty of misconduct, Thomas H. Maugh II. Los Angeles Times. 19.07.2008. https://www.latimes.com/archives/la-xpm-2008-jul-19-sci-misconduct19-story.html
[4] Prediction of Crosstalk Involving Twisted Pairs of Wires-Part I: A Transmission-Line Model for Twisted-Wire Pairs, Clayton R. Paul ; Jack W. McKnight. IEEE Transactions on Electromagnetic Compatibility, Volume: EMC-21, Issue: 2, May 1979.
[5] ETER Kick-Off Event: an ESR Perspective, Qazi Mashaal Khan. Cited on 18.03.2020. https://etn-peter.eu/2020/03/11/peter-kick-off-event-an-esr-perspective/
[6] Prediction of Crosstalk Involving Twisted Pairs of Wires-Part II: A Simplified Low-Frequency Prediction Model, Clayton R. Paul, Jack W. McKnight. IEEE Transactions on Electromagnetic Compatibility, Volume: EMC-21, Issue: 2, May 1979.
[7] Computation of the transmission line inductance and capacitance matrices from the generalized capacitance matrix, C. R. Paul, A. E. Feather. IEEE Transactions on Electromagnetic Compatibility, Volume: EMC-18, Issue: 4, Nov. 1976.
[8] Simulated NEXT and FEXT in twisted wire pair bundles, A. Shoory, M. Rubinstein, A. Rubinstein, F. Rachidi. 10th International Symposium on Electromagnetic Compatibility, York, UK. 26-30 Sept. 2011.
[9] Tiivistelmä matriisilaskennasta, Ossi Pasanen. v 3.5, 2.12.2008. http://www.courses.physics.helsinki.fi/teor/mapu/vanha/prujut/matriisitiivistelma-v3-5.pdf
About the Author: Oskari Leppäaho
Oskari accomplished his Master’s Degree in Electromagnetism at the Tampere University of Technology in Finland, 2015. Before joining the PETER project, he spent several years serving the industry on the fields of electromagnetic compatibility and electronics system design.
